Meting van variabiliteit: een overzicht

Meting van variabiliteit: een overzicht!

Betekenis van Variabiliteit:

Variabiliteit betekent 'Scatter' of 'Spread'. Dus maten van variabiliteit verwijzen naar de spreiding of verspreiding van scores rond hun centrale neiging. De variatiematen geven aan hoe de verdeling zich boven en onder de centrale tender verspreidt.

Uit het volgende voorbeeld kunnen we een duidelijk idee krijgen over het concept van variatiemaatstaven:

Stel dat er twee groepen zijn. In de ene groep zijn 50 jongens en in een andere groep 50 meisjes. Aan beide groepen wordt een test afgenomen. De gemiddelde score van jongens en is 54, 4 en meisjes is dat we de gemiddelde score van beide groepen vergelijken, we vinden dat er geen verschil is in de prestaties van de twee groepen. Maar stel dat de scores van de jongens variëren van 20 tot 80 en de scores van de meisjes variëren van 40 tot 60.

Dit verschil in bereik geeft aan dat de jongens meer variabel zijn, omdat ze meer grondgebied beslaan dan de meisjes. Als de groep personen bevat met zeer verschillende capaciteiten, zullen scores van hoog naar laag worden verspreid, het bereik zal relatief breed zijn en de variabiliteit zal groot worden.

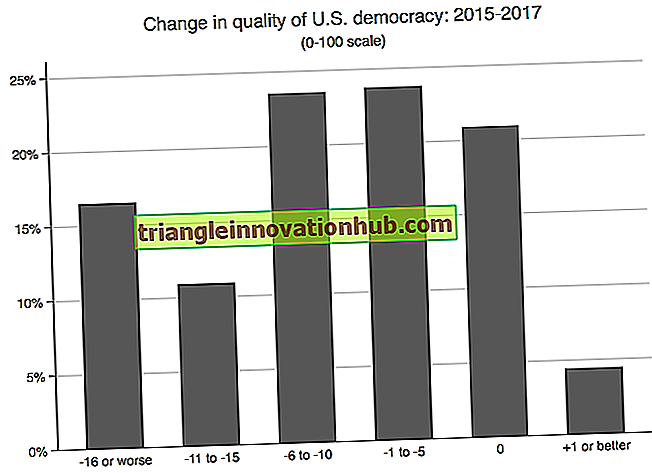
Deze situatie kan grafisch worden geïllustreerd in de onderstaande cijfers:

De bovenstaande afbeelding toont twee frequentieverdelingen van het enige gebied (N) en een gemiddelde (50) maar met een zeer verschillende variabiliteit. Groep A varieert van 20 tot 80 en Groep B van 40 tot 60 Groep A is drie keer zo variabel als groep-B - spreidt zich uit over drie keer de afstand op de schaal van scores, hoewel beide distributies de enige centrale neiging hebben.

Definities van Variabiliteit:

Woordenboek van Onderwijs-CV Goed. "De spreiding of variabiliteit van de waarnemingen van een verdeling over een zekere mate van centrale tendens." Collins Statistiekboek: "Verspreiding is de verspreiding van een verdeling"

AL Bowley:

"Dispersie is de maat voor de variatie van de items."

Brooks and Dicks:

"Verspreiding of spreiding is de mate van verstrooiing of variatie van de variabelen rond een centrale waarde." Dus de eigenschap die de mate aangeeft waarin de waarden worden verspreid over de centrale waarden, wordt dispersie genoemd. Het geeft ook het gebrek aan uniformiteit in de grootte van items van een distributie aan.

Behoefte aan variabiliteit:

1. Helpt om de maatstaf van afwijking te bepalen:

De variatiemaatstaven helpen ons om de mate van afwijking te meten die in de gegevens bestaat. Daarmee kunnen de grenzen worden bepaald waarbinnen de gegevens in een meetbare variëteit of kwaliteit marineren.

2. Het helpt om verschillende groepen te vergelijken:

Met behulp van validiteitsmetingen kunnen we de oorspronkelijke gegevens in verschillende eenheden vergelijken.

3. Het is nuttig de informatie aangevuld met de maatregelen van centrale tendentie aan te vullen.

4. Het is nuttig om verdere voorschotstatistieken te berekenen op basis van de spreidingsmaatstaven.

Maatregelen van Variabiliteit:

Er zijn vier variatiemaatregelen:

1. Het bereik

2. De kwartielafwijking

3. De gemiddelde afwijking

4. De standaarddeviatie

Dit zijn:

1. Het bereik:

Bereik is het verschil tussen in een reeks. Het is de meest algemene maat voor spreiding of verspreiding. Het is een maat voor variabiliteit van de variëteiten of observatie onderling en geeft geen idee over de spreiding van de waarnemingen rond een centrale waarde.

Bereik = H-L

Hier H = Hoogste score

L = laagste score

Voorbeeld:

In een klas hebben 20 studenten de cijfers als volgt behaald:

22, 48, 43, 60, 55, 25, 15, 45, 35, 68, 50, 70, 35, 40, 42, 48, 53, 44, 55, 52

Hier - De hoogste score is 70

De laagste score is 15

Bereik = H - L = 70 -15 = 55

Als het bereik groter is dan geeft de groep meer heterogeniteit aan en als het bereik lager is dan geeft de groep meer homogeniteit aan. Het bereik geeft ons een onmiddellijke en ruwe indicatie van de variabiliteit van een verdeling.

Verdiensten van bereik:

1. Bereik is gemakkelijk te berekenen en gemakkelijk te begrijpen.

2. Het is de eenvoudigste maatstaf voor variabiliteit.

3. Het geeft een snelle schatting van de mate van variabiliteit.

Demerits van bereik:

1. Bereik wordt sterk beïnvloed door fluctuatie van scores.

2. Het is niet gebaseerd op alle waarnemingen van de serie. Het neemt alleen de hoogste en de laagste scores in rekening.

3. In het geval van open einddistributies kan het bereik niet worden gebruikt.

4. Het wordt sterk beïnvloed door fluctuaties in bemonstering.

5. Het wordt sterk beïnvloed door extreme scores.

6. De serie wordt niet echt weergegeven door bereik. Een symmetrische en A-symmetrische verdeling kan hetzelfde bereik hebben, maar niet dezelfde spreiding.

Gebruik van bereik:

1. Bereik wordt gebruikt als een maat voor spreiding wanneer variaties in de waarde van de variabele niet veel zijn.

2. Bereik is de beste maatstaf voor variabiliteit wanneer de gegevens te verspreid of te summier zijn.

3. Range wordt gebruikt wanneer de kennis van extreme score of totale spreiding gewenst is.

4. Wanneer een snelle schatting van de variabiliteit gewenst is, wordt bereik gebruikt.

2. De kwartielafwijking (Q):

Naast bereik is de kwartielafwijking een andere maat voor de variabiliteit. Het is gebaseerd op het interval dat de middelste vijftig procent van de gevallen in een bepaalde verdeling bevat. Een kwart betekent 1/4 van iets, wanneer een schaal is verdeeld in vier gelijke delen. "De kwartielafwijking of Q is de helft van de schaalafstand tussen de 75t en 25e percentielen in een frequentieverdeling."

Uit de figuur 9.2 hebben we geconstateerd dat het 1e kwartiel of Q ₁ positie is in een verdeling waaronder 25% gevallen, en waarboven 75% gevallen liggen. Het 2e kwartiel of Q2 is een positie onder en waarboven 50% gevallen liggen. Het is de mediaan van de distributie.

Het derde kwartiel of Qg is het 75e percentiel, waaronder 75% gevallen en waarboven 25% gevallen liggen. De kwartielafwijking (Q) is dus de helft van de schaalafstanden tussen het 3e kwartiel (Q ₃ ) en het 1e kwartiel (Q ₁ ). Het is ook bekend als de Semi-Interquartile Rage.

Symbolisch:

Daarom moet de orde om de kwartielafwijking te berekenen eerst en vooral het 1e kwartiel (Q ₁ ) en het 3e kwartiel (Q ₃ ) berekenen

Waarbij = L = ondergrens van de 1e kwartielklasse,

De 1e kwartielklasse is die klasse waarvan de cumulatieve frequentie groter is dan de waarde van N / 4 wanneer if wordt berekend vanaf het laagste uiteinde.

N / 4 = een vierde van het totale aantal gevallen.

F = cumulatieve frequentie van het klasseninterval onder de

1e kwartielles.

Fq ₁ = de frequentie van de klasse Q ₁

i = Grootte van het klasse-interval 3N

Waarbij: L = ondergrens van de 3e kwartielklasse

De derde kwartielklasse is die klasse waarvan de cumulatieve frequentie ( Cf ) groter is dan de waarde van 3N / 4, dwz Cf> 3N / 4, wanneer Cf wordt berekend vanaf het laagste uiteinde.

3N / 4 = ¾ e van N of 75% van het totale aantal gevallen.

F = cumulatieve frequentie van de klasse onder de klasse.

fq ₂ = De frequentie van de Q ₃ -klasse.

i = Grootte van het klasse-interval.

Berekening van kwartiel uit groepsgegevens:

Voorbeeld:

Ontdek de kwartielafwijking van de volgende gegevens:

Stappen om kwartielafwijking te berekenen:

Stap 1:

Bereken N / 4, dwz 25% van de verdeling en 3N / 4, dwz 75% van de verdeling.

Hier -N = 50 dus N / 4 = 12, 5

en 3N / 4 = 37, 5

Stap 2:

Bereken de C f vanaf het onderste uiteinde. Zoals in tabel-9.1 kolom-3.

Stap 3:

Ontdek de klasse Q ₁ en Q ₃ .

In dit voorbeeld:

Ci, 60-64 is de klasse Q1 omdat de C f > N / 4

Ci 75-79 is klasse Q ₃ omdat

de Cf> 3N / 4

Stap 4:

Ontdek F voor Q _1- klasse en Q _3- klasse. In dit voorbeeld

F voor Q _1- klasse = 10

F voor Q3-klasse = 30 stappen

Stap 5:

Ontdek Q1 door de bovenstaande waarden in de formule te plaatsen.

Q ₁ = L + N / 4 - F / fq1 xi

Hier is L = 59, 5 omdat de exacte limieten van de Q1-klasse 60-64 59, 5-64, 5 zijn.

F = 10 de Cf onder de Q _1- klasse

Fq ₁ = 4: de exacte frequentie van de klasse Q ₁

i = 5, grootte van het klasse-interval

N / 4 = 12, 5

Nu Q ₁ = 59, 5+ 12, 5-10 / 4 x 5

= 59, 5 + 2, 5 / 4 x 5

= 59, 5 + 0, 63 x 5

= 59, 5 + 3, 13 = 62, 63

Stap 6:

Ontdek de Q ₃ door de waarden in de formule te zetten.

Hier L = 74, 5 omdat de exacte limieten van de Q ₃ -klasse 75-79 74, 5-79, 5 is.

F = 30 de Cf onder de Q _3- klasse.

3N / 4 = 37, 5

Fq ₁ = 8 de exacte frequentie van de Q ₃ -klasse.

i = 5 grootte van de klassenintervallen.

Q ₃ = 74, 5 + 37, 5-30 / 8 x 5

= 74, 5 + 7, 5 / 8 x 5 = 74, 5 + .94 x 5

= 74, 5 + 4, 7 = 79, 2

Stap 7:

Ontdek Q door de bovenstaande waarde in de formule te plaatsen.

Q = Q ₃ -Q 1/2 = 79.2 - 62.63 / 2

= 16, 5 / 2 = 8, 285 = 8, 29

Verdiensten van kwartielafwijking:

1. Kwartielafwijking is eenvoudig te berekenen en gemakkelijk te begrijpen.

2. Het is representatiever en betrouwbaarder dan bereik. In het geval van open-ended klassenintervallen wordt het gebruikt bij het bestuderen van dispersiemetingen.

3. In het geval van open-ended klassenintervallen wordt het gebruikt bij het bestuderen van dispersiemetingen.

4. Het is een goede index van scorendichtheid in het midden van de verdeling.

5. Wanneer we Mediane als maat voor de centrale neiging op dat moment nemen, heeft Q de voorkeur als maat voor de dispersie.

6. Hetzelfde bereik wordt niet beïnvloed door extreme scores.

Afwijkingen van de kwartielafwijking:

1. Het is niet gebaseerd op alle waarnemingen van gegevens. Het negeert de eerste 25% en de laatste 25% van de scores.

2. Verdere algebraïsche behandeling is niet mogelijk in het geval van Q. Het is slechts een positioneel gemiddelde. Het bestudeert geen variatie van de waarden van een variabele van een gemiddelde. Het geeft alleen een afstand op een schaal aan.

3. Het wordt beïnvloed door fluctuatie van scores. De waarde ervan wordt in elk geval beïnvloed door een verandering in de waarde van een enkele score.

4. Q is geen geschikte spreidingsmaatstaf, wanneer er in een reeks een aanzienlijke variatie is in de waarden van verschillende scores.

Gebruik van kwartielafwijking:

1. Wanneer Mediane de maat is van centrale neiging in die tijd, wordt Q gebruikt als de maat voor dispersie.

2. Wanneer extreme scores van invloed zijn op SD of de scores op dat moment worden verspreid, wordt Q gebruikt als maat voor de variabiliteit.

3. Als het ons in de eerste plaats gaat om de concentratie rond de mediaan - de middelste 50% van de gevallen - wordt Q gebruikt.

4. Als de klassenintervallen open einde hebben, wordt Q gebruikt als maat voor de spreiding.

3. De gemiddelde afwijking (AD):

We hebben gesproken over variabiliteit van twee variaties, bereik en kwartiel. Maar geen van deze spreiding geeft aan over de samenstelling van de verdeling. Dit komt omdat beide dispersies niet alle individuele scores in aanmerking nemen. We kunnen enkele van de ernstige tekortkomingen van bereik- en kwartielafwijkingen overwinnen door een andere dispersie te gebruiken die Gemiddelde afwijking of Gemiddelde afwijking wordt genoemd.

"Gemiddelde afwijking is het rekenkundig gemiddelde van alle afwijkingen van verschillende scores van de gemiddelde waarde van de scores zonder rekening te houden met het teken van de afwijking."

Dus het rekenkundig gemiddelde van de gemiddelde deviatie van de afwijkingen van een reeks berekend op basis van een zekere mate van centrale tendens. Dus gemiddelde afwijking is het gemiddelde van de afwijkingen van hun gemiddelde (soms van mediaan en modus).

Definities:

Collins Woordenboek van statistieken:

"Gemiddelde afwijking is het gemiddelde van de absolute waarden van de verschillen tussen de waarden van een variabele en het gemiddelde van de verdeling."

Woordenboek van het onderwijs, CV Goed:

"Een maatstaf die de gemiddelde waarde uitdrukt waarmee de afzonderlijke items in een distributie afwijken van een maat voor de centrale tendens, zoals het gemiddelde van de mediaan."

HE Garrett:

"De gemiddelde afwijking of AD is het gemiddelde van de afwijkingen van alle afzonderlijke scores in een reeks van hun gemiddelde (af en toe van de mediaan of modus)."

Dus kan worden gezegd dat de gemiddelde afwijking of de gemiddelde afwijking zoals deze wordt genoemd, het gemiddelde is van de afwijkingen van alle scores.

Er wordt geen rekening gehouden met tekenen en alle afwijkingen, of + ve of -ve behandeld als positief.

waar AD = Gemiddelde afwijking

£ = Capital Sigma, Mean Sum total of

II = Modulous in het kort Mod, betekent geen respect voor negatief teken.

x = afwijking, (X-M)

Berekening van de gemiddelde afwijking:

Er zijn twee situaties voor het berekenen van de gemiddelde afwijking:

(a) Wanneer gegevens niet gegroepeerd zijn.

(b) Wanneer gegevens zijn gegroepeerd.

Berekening van AD uit niet-gegroepeerde gegevens.

Voorbeeld:

Zoek AD van de volgende 10 scores hieronder:

23, 34, 16, 27, 28, 39, 45, 26, 18, 27

Oplossing:

Stap 1:

Ontdek het gemiddelde van de scores met de formule

ΣX / N

Stap 2:

Ontdek de afwijking van alle scores die het gemiddelde van de scores aftrekken.

Stap 3:

Ontdek de absolute afwijking zoals weergegeven in tabel 9.2 en dan Σ | x |

Stap 4:

Zet de waarden in de formule.

De AD = 7, 58.

Berekening van AD uit gegroepeerde gegevens:

Voorbeeld:

Ontdek de AD van de volgende gegevens:

Oplossing :

Stap 1:

Ontdek het gemiddelde van de distributie.

Gemiddelde = 70, 80

Stap 2:

Ontdek het middelpunt voor elke klasse-interval. Zoals in kolom -3 van tabel -9.3

Stap 3:

Ontdek de x door het gemiddelde van het middelpunt (X) af te trekken. Zoals getoond in kolom -5 van tabel 9.3.

Stap 4:

Ontdek absolute afwijking of | x |. Als kolom -6 hierboven.

Stap 5:

Ontdek het f x |. door f te vermenigvuldigen met | x. Zoals getoond in kolom -7 en ontdek Σ | f x |.

Stap 6:

Zet de bovenstaande waarden in de formule.

De formule voor AD uit gegroepeerde gegevens

Waar = AD = Gemiddelde afwijking

Σ = Totaal som van

f = frequentie

x = afwijking ie (X-M)

N = Totaal aantal gevallen, dwz Σ f .

De waarden in de formule plaatsen

Verdiensten van AD:

1. Gemiddelde afwijking is rigide gedefinieerd en de waarde ervan is nauwkeurig en definitief.

2. Het is gemakkelijk te berekenen.

3. Het is gemakkelijk te begrijpen. Omdat het het gemiddelde is van de afwijkingen van een maat voor centrale tendentie.

4. Het is gebaseerd op alle waarnemingen.

5. Het wordt minder beïnvloed door de waarde van extreme scores.

Demerits van AD:

1. Het meest ernstige nadeel van de gemiddelde afwijking is dat het de algebraïsche tekens van de afwijkingen negeert die indruisen tegen de fundamentele regels van de wiskunde.

2. Verdere algebraïsche behandeling is niet mogelijk in het geval van AD.

3. Het wordt zeer zelden gebruikt. Vanwege standaardafwijking wordt over het algemeen gebruikt als een maat voor dispersie.

4. Wanneer berekend vanuit de modus AD wordt geen nauwkeurige meting van de spreiding gegeven.

Gebruik van gemiddelde afwijking:

1. Gemiddelde afwijking wordt gebruikt wanneer het gewenst is om alle afwijkingen van het gemiddelde te wegen op basis van hun grootte.

2. Wanneer extreme scores de standaarddeviatie op dat moment beïnvloeden, is AD de beste spreidingsmaatstaf.

3. AD wordt gebruikt wanneer we willen weten in hoeverre de maatregelen aan weerszijden van het gemiddelde worden verspreid.

4. De standaarddeviatie (SD):

We hebben drie variatiemaatstaven besproken, namelijk Bereik, Kwartielafwijking en Gemiddelde Afwijking. We hebben ook vastgesteld dat ze allemaal ernstige nadelen hebben.

Het bereik dat zojuist is opgenomen om alleen de hoogste score en de laagste score te verantwoorden. De kwartielafwijking houdt alleen rekening met de middelste 50% van de scores en in het geval van gemiddelde afwijking negeren we de tekens.

Daarom gebruiken we, om al deze moeilijkheden te overwinnen, een andere dispersiemethode genaamd Standaardafwijking. Het wordt vaak gebruikt in experimenteel onderzoek, omdat het de meest stabiele variabiliteitsindex is. Symbolisch wordt het geschreven als σ (Griekse kleine letter sigma).

Definities:

Collin's Woordenboek van Statistieken.

"Standaardafwijking is een maat voor spreiding of verspreiding. Het is root mean squared deviation. "

Woordenboek van Onderwijs-CV Goed.

"Een veel gebruikte maat voor variabiliteit, bestaande uit de vierkantswortel van het gemiddelde van de gekwadrateerde afwijkingen van scores van het gemiddelde van de verdeling."

Standaardafwijking is de vierkantswortel van de gemiddelde waarde van de gekwadrateerde afwijkingen van de scores van hun rekenkundig gemiddelde.

De SD wordt berekend door de gekwadrateerde afwijking van elke maat van het gemiddelde op te tellen, gedeeld door het aantal gevallen en de vierkantswortel uit te pakken. Voor alle duidelijkheid, we moeten hier opmerken dat we bij het berekenen van de SD alle afwijkingen afzonderlijk verdelen, hun som vinden, de som delen door het totale aantal scores en dan de vierkantswortel vinden van het gemiddelde van de gekwadrateerde afwijking. Zodat het ook de 'wortelgemiddelde vierkante afwijking' wordt genoemd.

Het vierkant met standaarddeviatie wordt Variantie genoemd (σ ² ). Het wordt de gemiddelde vierkante afwijking genoemd. Het wordt ook wel het tweede moment dispersie genoemd.

Berekening van SD van niet-gegroepeerde gegevens:

Voorbeeld:

Ontdek de SD van de volgende gegevens:

6, 8, 10, 12, 5, 8, 9, 17, 20, 11.

Oplossing:

Stap 1:

Ontdek het gemiddelde van de scores.

Stap 2:

Ontdek de afwijking (x) van elke score.

Berekening van SD uit gegroepeerde gegevens:

In gegroepeerde gegevens kan SD op twee manieren worden berekend:

1. Directe methode of Lange methode

2. Korte methode of veronderstelde gemiddelde methode

1. Directe methode of Lange methode:

Voorbeeld:

Ontdek de SD van de volgende distributie:

Oplossing:

Stap 1:

Ontdek het middelpunt van elk klasseninterval. (Colum-3 tabel 9.4)

Stap 2:

Ontdek het gemiddelde van de verdeling:

Hier M = Σ f x / N = 3540/50

= 70, 80

Stap 3:

Ontdek de afwijking (x) door het gemiddelde van punten af te trekken.

Stap 4:

Ontdek de f x door de f (col-2) te vermenigvuldigen met x (col-5)

Stap 5:

Ontdek de f x door f x (col-2) te vermenigvuldigen met x (col-5)

Stap 6:

Bereken Σ f x door de waarden in col-7 toe te voegen.

Stap 7:

Zet de waarden in de formule.

2. Korte methode of aangenomen gemiddelde methode:

Kort gezegd, de methodeberekening van SD is eenvoudig en minder tijdrovend. Als de middelpunten van de klassenintervallen decimale getallen zijn, wordt het ingewikkelder om SD te berekenen in de lange methode. Deze methode bestaat hoofdzakelijk uit 'gissen' of het aannemen van een gemiddelde en het later toepassen van een correctie om het werkelijke gemiddelde te geven. Zodat het als veronderstelde gemiddelde methode wordt genoemd.

Voorbeeld:

Bereken de SD, van de volgende verdeling:

Oplossing:

Stap 1:

Ga uit van het middelpunt van elk klasse-interval als 'Aangenomen gemiddelde'. Maar het is beter om te veronderstellen dat het middelpunt van het klasse-interval in het midden de hoogste frequentie heeft als aangenomen gemiddelde. Hier wordt verondersteld = 72 als verondersteld gemiddelde.

Stap 2:

Ontdek x (afwijking van de scores van het veronderstelde gemiddelde) zoals getoond in col-3.

x '= X - M / i

Stap 3:

Bereken f x ', door x' te vermenigvuldigen met f (col-4).

Stap 4:

Bereken f x ² door x '(col-3) te vermenigvuldigen met f x (col-5).

Stap 5:

Ontdek Σ f x 'en Σ f x ' ² it 'door de waarden toe te voegen in respectievelijk col-4 en col-5. '

Stap 6:

Zet de waarden in formule:

Formule voor SD in korte methode is:

Waarbij i = Grootte van het klasse-interval

Σ = Totaal som van

f = frequentie

x '= afwijking van de scores van hun veronderstelde gemiddelde.

Als we nu Σ f x '/ N vervangen in plaats van C.

De formule is als volgt:

Nu zetten we de waarden in de formule die we krijgen.

1.Als een constante waarde aan elke score wordt toegevoegd of van elke score wordt afgetrokken, blijft het dal van SD onveranderd:

Het betekent dat SD onafhankelijk is van verandering van oorsprong (optellen, aftrekken). Dus als een constante waarde wordt toegevoegd of afgetrokken van elke variëteit, blijft de SD hetzelfde.

We kunnen dit vanuit het volgende voorbeeld bekijken:

In de bovenstaande tabel worden scores van 5 studenten gegeven. Laten we eens kijken wat er gebeurt met de SD van de scores als we een constant getal 5 toevoegen en 5 van elke score aftrekken.

2. Als een constante waarde wordt vermenigvuldigd of gedeeld tot de oorspronkelijke scores, wordt de waarde van SD ook vermenigvuldigd of gedeeld door hetzelfde aantal:

Het betekent dat de SD onafhankelijk is van schaalverandering (vermenigvuldiging, deling). Als we de originele scores vermenigvuldigen met een constant getal, wordt de SD ook vermenigvuldigd met hetzelfde aantal.

Nogmaals, als we elke score verdelen met een constant getal, wordt de SD ook gedeeld door hetzelfde aantal.

We kunnen dit illustreren met het volgende voorbeeld:

In de bovenstaande tabel worden scores van 5 studenten gegeven. Laten we eens kijken wat er gebeurt met de SD van de 5 scores als we het vermenigvuldigen met een constant getal, zeg 2 en delen met hetzelfde constante getal.

Hieruit bleek dat als de scores worden vermenigvuldigd met een constant getal, de σ ook daarmee wordt vermenigvuldigd. Als de scores worden gedeeld door een constant getal, wordt de σ ook gedeeld door hetzelfde aantal.

Verdiensten van SD:

1. Standaardafwijking is rigide gedefinieerd en de waarde ervan is altijd definitief.

2. Het is gebaseerd op alle waarnemingen van gegevens.

3. Het is in staat tot verdere algebraïsche behandeling en bezit vele wiskundige eigenschappen.

4. In tegenstelling tot Q en AD wordt het minder beïnvloed door fluctuaties van scores.

5. In tegenstelling tot AD negeert het de negatieve signalen niet. Door kwadraten van afwijkingen op te lossen, overwint het deze moeilijkheden.

6. Het is de betrouwbare en meest nauwkeurige maatstaf voor variabiliteit. Het gaat altijd met het gemiddelde dat de meest stabiele maat voor de centrale neiging is.

7. SD geeft een meetwaarde die van de ene test tot de andere vergelijkbaar is. Vooral de normale curve-eenheden worden uitgedrukt in een eenheid.

Demerits van SD:

1. SD is moeilijk te begrijpen en niet eenvoudig te berekenen.

2. SD geeft meer gewicht aan extreme scores en verliezen dan die welke dichter bij het gemiddelde liggen. Omdat de kwadraten van de afwijkingen, die groot zijn, proportioneel groter zijn dan de vierkanten van die afwijkingen die relatief klein zijn.

Gebruik van SD:

1. SD wordt gebruikt wanneer onze stuwkracht is om de variabiliteit met de grootste stabiliteit te meten.

2. Wanneer extreme afwijkingen de variabiliteit op dat moment kunnen beïnvloeden, wordt SD gebruikt.

3. SD wordt gebruikt voor het berekenen van de verdere statistieken zoals correlatiecoëfficiënt, standaardscores, standaardfouten, variantieanalyse, analyse van co-variantie enz.

4. Wanneer de interpretatie van scores wordt gemaakt in termen van de NPC, wordt SD gebruikt.

5. Wanneer we de betrouwbaarheid en validiteit van testscores willen bepalen, wordt SD gebruikt.

Gecombineerde standaarddeviatie:

Tijdens het onderzoekswerk trekken we soms meer dan één steekproef uit de populatie. Daarom krijgen we voor elke groep of steekproef verschillende SD's. Maar soms moeten we deze resultaten interpreteren als één groep. Daarom is het mogelijk, wanneer verschillende sets scores zijn samengevoegd tot een enkele partij, de SD van de totale verdeling van de SD's van de subgroepen te berekenen.

Formule voor het berekenen van gecombineerde standaardafwijking of is als volgt: